Empirical Exercise 10
This is the first of two exercises on power calculations. In this exercise, we’ll learn how to calculate the minimum detectable effect as a function of sample size (or the required sample size as a function of the minimum detectable effect).
Getting Started
The minimum detectable effect or MDE is the smallest impact that we can detect with probability 0.8. The MDE
depends on the sample size (N), the proportion of the sample assigned to treatment (P), and the
standard deviation of our outcome of interest. We can calculate the MDE using the formula:
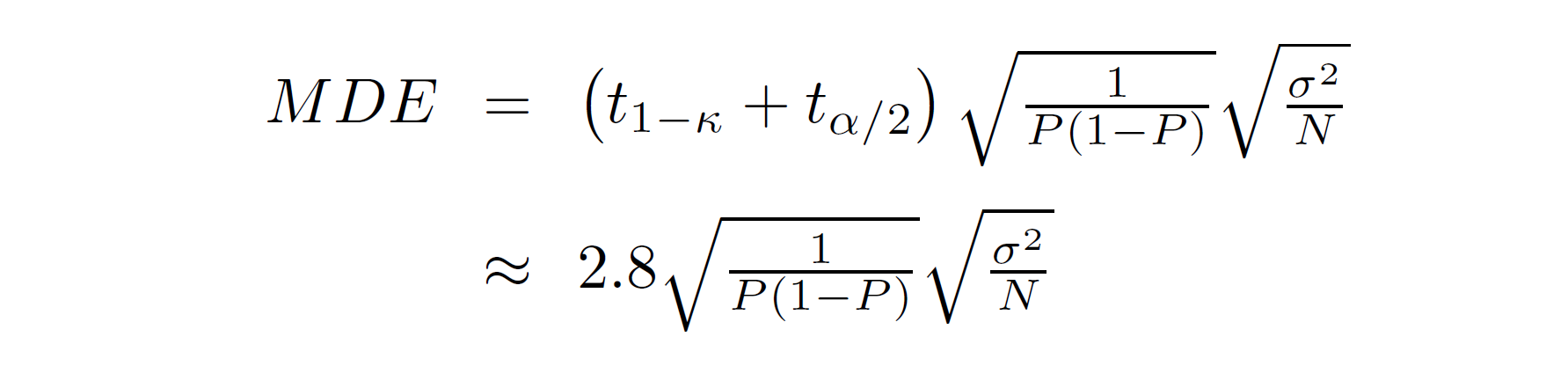
We’ll be using data from two experiments that we’ve already studied. The first of these is the impact evaluation of malaria treatment that we studied in the first week of class. The data set E1-CohenEtAl-data.dta contains data from Price Subsidies, Diagnostic Tests, and Targeting of Malaria Treatment: Evidence from a Randomized Controlled Trial by Jessica Cohen, Pascaline Dupas, and Simone Schaner. We will also use data from the paper The Miracle of Microfinance? Evidence from a Randomized Evaluation by Abhijit Banerjee, Esther Duflo, Rachel Glennerster, and Cynthia Kinnan. We sued this latter data set in Empirical Exercises 6 and 9.
Question 1
Your are designing an intervention intended to increase knowledge about malaria transmission, using
the data set E1-CohenEtAl-data.dta. Your
main outcome variable of interest is the variable b_knowledge_correct, which measures beliefs about how malaria
is transmitted and what can be done to treat it. Familiarize yourself with this variable: what is
its mean, and what are the maximum and minimum values observed in the sample?
Write Stata code that summarizes b_knowledge_correct, using the sum command with the detail option
so that the standard deviation is saved as a local after you run the command. What is the estimated standard deviation of
b_knowledge_correct? Write an additional line of code to display the MDE given the standard deviation of
b_knowledge_correct and the sample size, if you assume that the treatment and comparison groups are
the same size (so P in the MDE formula = 0.5). What is the MDE?
Question 2
You can also calculate the sample size needed to detect a particular MDE using Stata sampsi command. Type the command:
sampsi 0 0.11651129, power(0.8) sd(0.4989005)
What sample size does Stata suggest, and how does it compare to the actual sample size (that you used to calculate the MDE in Question 1)?
Question 3
The treatment dummy in the original study is act_any. Based on this variable, what is the ratio
of treated obesrvations to control observations? What proportion of the sample was assigned to treatment?
Use the formula to calculate the MDE in the study (if you used the same outcome variable as above,
b_knowledge_correct) given the actual ratio of treatment to control observations. What is the MDE?
Question 4
How large of a sample size would need to detect the MDE that you calculated in Question 1?
Question 5
Now we will consider a completely different data set: the data on access to microfinance that we used in Empirical Exercise 6 and again in Empirical Exercise 9. We are going to use the variable bizprofit_1, which measures microenterprise profits. Unlike the knowledge variable used above, the standard deviation of bizprofit_1 is large relative to its mean.
What is the mean of bizprofit_1? What is the standard deviation of bizprofit_1?
Part (a)
Given the size of this data set and the standard deviation of bizprofit_1, what is the MDE if you wanted to have power of 0.8 (assuming treatment and comparison groups of equal size)? How does this MDE compare to the mean of the outcome variable? How large of a percent change in the outcome would you need to anticipate if you wanted to have power of at least 0.8?
Part (b)
If you wanted to have power of 0.8 to detect a 25 percent increase in business profits, how large of a sample size would you need?
This exercise is part of the module Power Calculations.