Empirical Exercise 7, Part 2

In this exercise, we’ll be using a data set on school enrollment in 15 African countries that eliminated primary school fees between 1990 and 2015. Data on enrollment comes from the World Bank’s World Development Indicators Database. We’ll be using these data to estimate the two-way fixed effects estimator of the impact of eliminating school fees on enrollment. Since this policy was phased in by different countries at different time, it is a useful setting for exploring the potential pitfalls of two-way fixed effects.

Getting Started

Start by creating a do file that downloads the data from the course website. Your code will look something like this:

clear all 
set scheme s1mono 
set more off
set seed 12345
webuse set https://pjakiela.github.io/ECON379/exercises/E7-TWFE/
webuse E7-TWFE-data.dta

The data set only contains six variables: country, year, id, gross_enrollment, net_enrollment, and fpe_year. The variables country and year are self-explanatory. id is a unique numeric identifier for each of the 15 individual countries in the data set. The variable fpe_year indicates the year in which a given country made primary schooling free to all eligible children. Malawi was the first country in the data set that eliminated primary school fees (in 1994), while Namibia was the last (in 2013). The countries in the data set and the timing of school fee elination is summarized in the table below.

ID	Country	Implementation of Free Primary Education
27	Malawi	1994
17	Ethiopia	1995
20	Ghana	1996
46	Uganda	1997
7	Cameroon	2000
44	Tanzania	2001
47	Zambia	2002
35	Rwanda	2003
23	Kenya	2003
5	Burundi	2005
31	Mozambique	2005
24	Lesotho	2006
2	Benin	2006
4	Burkina Faso	2007
32	Namibia	2013

The data set contains 15 countries, but only 13 distinct “timing groups” - since Kenya and Rwanda both eliminated primary school fees in 2003, while Benin and Lesotho both eliminated fees in 2006.

The data set also contains the the variables gross_enrollment and net_enrollment which provide two closely related measures of school participation. The gross primary enrollment ratio is 100 times the number of students enrolled in primary school divided by the number of primary-school aged children. This number can be greater than 100 when over-age children are enrolled in primary school - which often happens when school fees are eliminated. The net primary enrollment ratio is 100 times the number of primary-school aged children enrolled in primary school divided (again) by the total number of primary-school aged children. The net primary enrollment ratio should not be greater than 100.

Start by familiarizing yourself with the data set. What are the first and last years included in the sample? Which countries eliminated school fees in the 1990s? How many countries eliminated primary school fees after 2010?

We are going to be looking at the outcome variable gross_enroll, but this variable is missing for some country-years. How many? Go ahead and drop those observations to make your life easier.

The Mechanics of Two-Way Fixed Effects

Now we are ready to estimate the impact of eliminating primary school fees on gross enrollment using two-way fixed effects. We want to implement the regression equation:

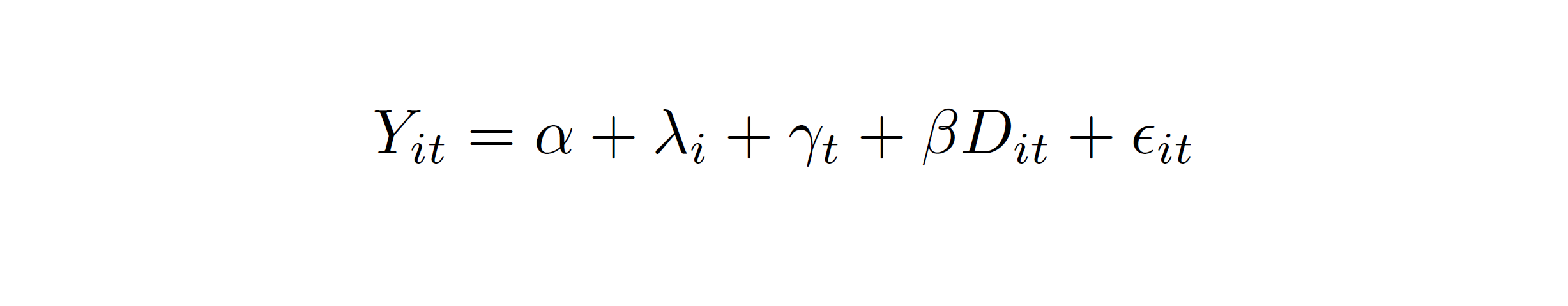
where Y_it is the outcome variable of interest (gross enrollment); λ_i and γ_t are country and time fixed effects, respectively; and D_it is the treatment dummy, an indicator equal to one in country-years after the elimination of school fees (inluding the year during which school fees were eliminated).

Extend your do file to generate the variable D_it (you may wish to call it treatment) and then run the two-way fixed effects regression of gross enrollment on your dummy for free primary education. What is the estimated coefficient on treatment? Is it statistically significant?

Note: you cannot include the code i.country to generate fixed effects for individual countries because Stata will not generate fixed effects for the different values of a string variable. What is a string variable? A variable with values that are combinations of letters and numbers, as opposed to variables that only take on numeric values. Use the country ID variable id when you want to include country fixed effects.

The coefficient from a two-way fixed effects regression is equal to the coefficient from a regression of your outcome on the residuals from a regression of treatment on your two-way fixed effects. To see this, regress treatment on country and year fixed effects, and the use the post-estimation predict command to generate a value equal to the residual from this regression:

reg treatment i.year i.id
predict tresid, resid

In the command above, tresid is the name of my new variable, a variable that is the residual from a regression of treatment on country and year fixed effects. Regress gross_enrollment on tresid without any additional controls. You should see that the estimated coefficient is identical to the coefficient of interest in your original two-way fixed effects regression.

We can also calculate the difference-in-differences estimator “by hand” from the observed values of the gross_enroll and tresid variables. We know that when we run a univariate regression in a data set containing a totla of n observations, the OLS coefficient can be written as:

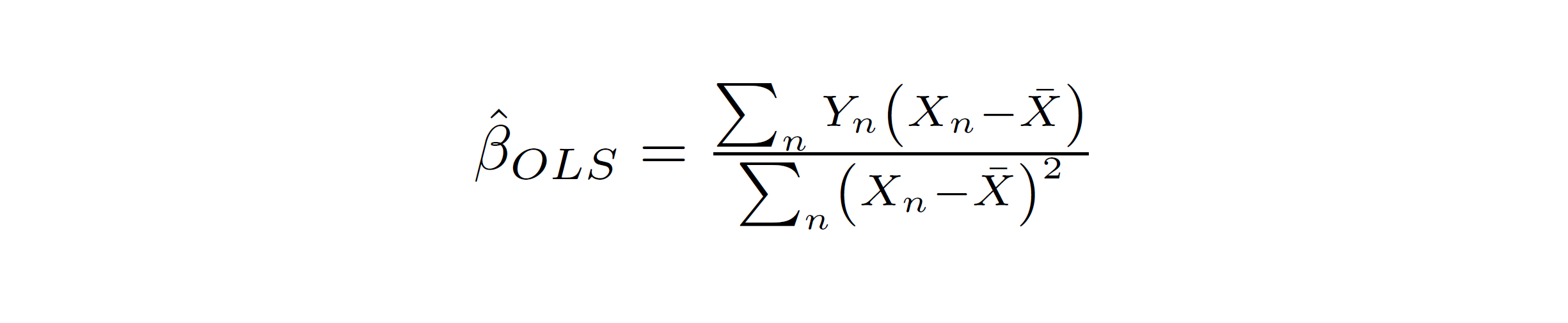
In this case, our right-hand side variable (X in the equation above) is the residualized treatment variable tresid. It has a mean of zero (the residuals from a regression are mean-zero by construction) - so we don’t need to worry about the “X-bar” terms. This means that we can calculate the two-way fixed effects difference-in-differences estimator using the following code:

gen yxtresid = gross_enroll*tresid
egen sumyxtresid = sum(yxtresid)
gen tresid2 = tresid^2
egen sumtresid2 = sum(tresid2)
gen twfecoef = sumyxtresid/sumtresid2
sum twfecoef
display r(mean)

In the first line, we calculate a variable that is the value of the outcome variable multiplied by the associated residual from a regression of treatment on country and year fixed effects. We then use the egen command to sum these terms across all observations. In the next two lines, we sum up the observation-level values of the square of our residualized treatment variable. The last three lines use these two sums - which appear in the algebra above - to caluculate the TWFE estimator of the treatment effect by hand (in some sense).

If you have done this correctly, you will see that our original two-way fixed effects coefficient, the coefficient from our regression of gross_enroll on tresid, and the mean of our new variable twfecoef are all identical (though the associated standard errors are different). Thus, we’ve shown that the two-way fixed effects coefficient is a weighted sum of the values of the outcome variable (like any coefficient from a univariate OLS regression).

Is the Two-Way Fixed Effects Coefficient Biased?

In lecture, we saw that the two-way fixed effects difference-in-differences estimator does not always provide an unbiased estimate of the treatment effect that we are interested in. We can now see why. We started with a treatment dummy: treatment in country-years where primary education was free, and zero in country-years when primary school fees had not yet been eliminated. So, our treatment group is the
country-years with free primary education.

However, when we include country and year fixed effects, we convert our treatment dummy into a continuous measure of treatment intensity - specifically a measure of treatment intensity that is not explained/predicted by the country year fixed effects.

There is an important difference between regression on a dummy variable and regression on a continuous measure of treatment intensity (as we saw in earlier modules): when we regress on (only) a treatment dummy, the estimated treated effect is a weighted average of the treatment effect on treated units (assuming there is no selection bias to worry about); but when we regress on a continous measure of treatment intensity, we are imposing a linear dose-response relationship and placing greater weight on outcomes further from the mean treatment intensity. Importantly, all observations with below mean treatment intensity are implicitly part of the control group.

In practical terms, we’ve seen that the two-way fixed effects coefficient put negative weight on obesrvations where the residualized value of treatment (tresid) is negative. So, the practical question is: how often does this happen among obersvations with treatment equal to one? Test this by summarizing the tresid variable in the treatment group. What is the lowest value of tresid that you observe in the treatment group? How many treated observations are there, and how many of them have values of tresid that are less than zero?

You can use the following code to compare the distributions of the the tresid variable in the treatment and comparison groups:

tw ///
	(histogram tresid if treatment==0, frac bcolor(vermillion%40)) ///
	(histogram tresid if treatment==1, frac bcolor(sea%60)), ///
	xtitle(" " "Residualized Treatment") ///
	legend(label(1 "Comparison") label(2 "Treatment") col(1) ring(0) pos(11)) ///
	plotregion(margin(vsmall))

We can see that the residualized value of treatment is negative for quite a few country-years in the treatment group (where primary education was free). We know from lecture that this occurs because the value of treatment predicted from our regression of treatment on country and year fixed effects is greater than one. Hence, country-year observations receiving negative weight in our two-way fixed effects regression are those in countries where the mean level of treatment is high (early adopters of free primary education) in years when the average level of treatment is high (later years, after most countries implemented free primary education).

To confirm that this is the case, generate a variable negweight equal to one if a country-year has treatment==1 and tresid<0.
Tabulate the country variable among observations where this negweight variable is equal to one. Which country has the highest number of treated years receiving negative weight in our two-way fixed effects estimation? When did that country implement free primary education?

Of course, negative weights aren’t necessarily a problem. The question is whether the assumption of a linear relationship between the residualized outcome variable and the residualized treatment variable is reasonable. One way to explore the issue is by plotting these residuals, for example by using the code:

reg gross_enroll i.year i.id
predict yresid, resid
tw ///
	(scatter yresid tresid if treatment==0, msymbol(o) color(vermillion%20)) ///
	(scatter yresid tresid if treatment==1, msymbol(o) color(sea%20)) ///	
	(lpoly yresid tresid if treatment==0, lcolor(vermillion) lpattern(longdash) deg(1) bwidth(0.2)) ///
	(lfit yresid tresid if treatment==0, lcolor(vermillion) lpattern(solid)) ///	
	(lpoly yresid tresid if treatment==1, lcolor(sea) lpattern(longdash) deg(1) bwidth(0.2)) ///
	(lfit yresid tresid if treatment==1, lcolor(sea) lpattern(solid)), ///	
	legend(off)

In this case, we see that the assumption of a linear relationship between the residualized outcome variable and the residualized treatment variable does not seem unreasonable. In particular, we see that the slope of the linear fit is similar in the treatment and comparison groups. We can test this formally by regressing yresid on tresid, treatment, and an interaction between treatment and tresid. Are the coefficients on the treatment variable or interaction term statistically significant?

Truncating the Data Set to Eliminate Negative Weights

Negative weights arise because the predicted value of treatment is greater than one for some treated observations. This occurs for country-years where both the country-level-mean and the year-level-mean of the treatment variable are high - ie in early-adopter countries observed in later years of the panel (by which time most countries are treated). One way to eliminate negative weights, so that we only place positive weight on treated country-years, is to truncate the data set before late-adopted countries are treated. If treatment effects are homogenous, this should not change your estimated treatment effect too much (though your data set will be smaller, so your standard errors will probably be larger).

To see that this is the case, re-run your code (or add code to your do file that clear the data set and reloads the raw data) so that you drop observations after 2005. Re-run the two-way fixed effects estimation. What is the estimated coefficient on treatment? How different is it from your initial estimate (at the very beginning of this exercise)?

Now regress treatment on your country and year fixed effects, and then predict the residuals. These are the weights used in your two-way fixed effects estimation of the impact of treatment on school enrollment. Summarize the regression weights for observations in the treatment group. How many are negative? What is the lowest weight placed on a country-year observation where treatment==1?

Empirical Exercise

Now use your do file to answer the following questions:

1. What is the two-way fixed effects estimate of the impact of eliminated primary school fees on gross_enrollment?
2. How many observations in the treatment group (with treatment equal to one) receive negative weight in the two-way fixed effects estimation of the impact of free primary on gross_enrollment?
3. Regress the yresid variable generated above on tresid, treatment, and an interaction between tresid and treatment. What is the estimated OLS coefficient on the interaction term?
4. Is that interaction statistically significant? What is the associated p-value from the regression above?
5. What is the two-way fixed effects estimate of the impact of eliminated primary school fees on gross_enrollment if you only include data from 1981 through 2005?
6. When you only include data from 1981 through 2005, How many observations in the treatment group (with treatment equal to one) receive negative weight in the two-way fixed effects estimation of the impact of free primary on gross_enrollment?